|
過去ログ(2005.12.01〜2006.12.17)百件
| 2005年12月30日 友人からクイズが 2005.01.10解答編を補稿
|
|
友人から携帯メールでクイズが届きました。
「【問題】
ここに1枚の紙がある。 道具は何も使わずに、折るだけで1つの直角を3等分するにはどのように
すれば良いだろうか?」
…おや?
これって中学校で習った、「代表的な三角形の辺の比率」を当て嵌めてイイのかな?
あの、「辺の比率が1:2:√3の直角三角形は、内角が30°、60°、90°になる」という。
だとしたらメチャ簡単なんですが。
・
・
・
と
思
っ
た
の
で
す
が
・
・
・
・
・
・
正
解
は
、
そ
れ
と
は
違
う
ら
し
い
・
・
・
おいらのファクシミリが壊れていて、友人がスキャナを持っていないからメールに添付して送ってくれ
ることも出来ない(てゆーか、セキュリティを一時的に解除しないと添付ファイルが受け取れないからウザイ)ので、解答
を記した書面を郵送してもらうことにしました。
正答は、正月明けにココに記す予定です。 乞うご期待(というか、オイラが期待しまくっちゃっています)。
聞いた答えに我が耳を疑っちゃいました。
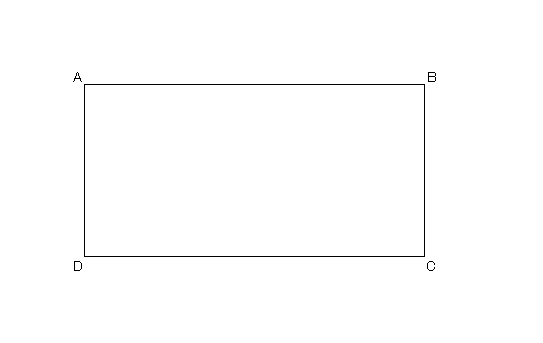
(1)一旦、長手方向に二つ折りして、再び開く。
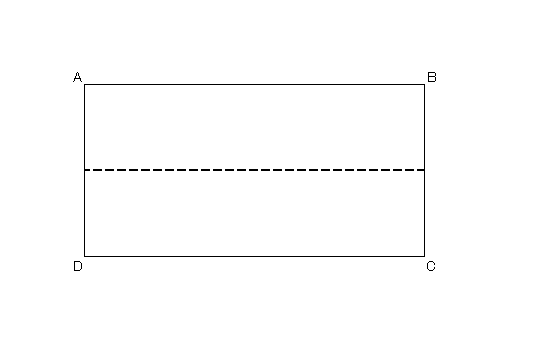
(2)ひとつの角を軸にして、もうひとつの角を真ん中の二分割線に合わせて折る。
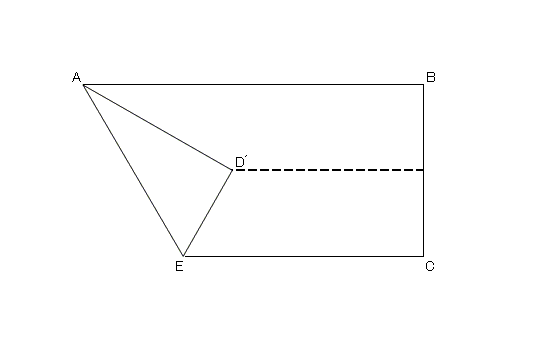
…たったこれだけ。
たったこれだけの作業で、
∠BAD´=∠D´AE=∠EAD
となって直角∠BADが三等分されたんですね。
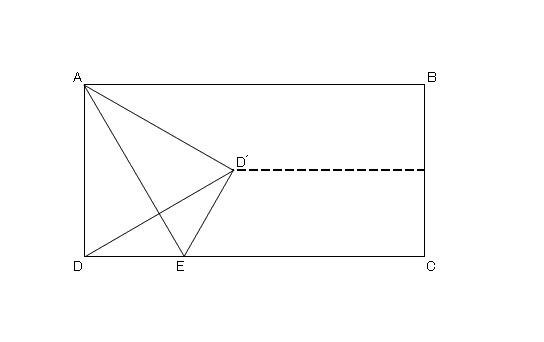
あまりにも華麗なので、一瞬ワケ判らなくなっちゃうヒトも居るんじゃないかと思いますが、中身は中学
レベルの幾何で至極簡単。
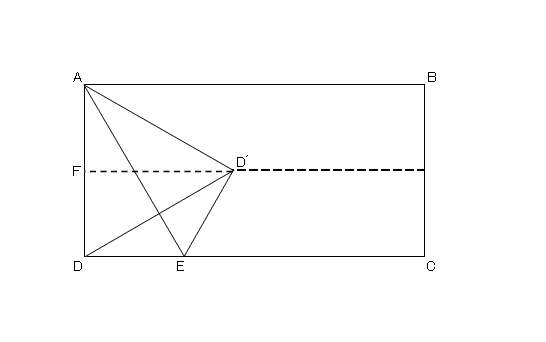
辺ADと辺AD´の長さは同じ。
ゆえに、△AFD´=△DFD´
ゆえに、△ADD´は正三角形。
ゆえに、∠DAD´は60度。
また、辺ADと辺AD´の長さ、および辺DEと辺ED´の長さは同じ。
ゆえに、△ADE=△AD´E
ゆえに、辺AEは、∠DAD´を二等分する。
∠DAD´は60度であったから、∠EADおよび∠EAD´は30度。
∠BADは90度であるから、∠BAD´は、90-30-30=30度。
よって、直角∠BADは、辺AEと辺AD´によって三等分される。
…ってダケの話。
仕組みは至極簡単なのだけど、普通思い付かないよなぁ。
|
|
|
|